What's going on here? 

Hint: ask yourself why longer levers generate more force
​
Bonus question: from a kinematic chain perspective, what is the bar count of this linkage?

Build pictures are here.

Why can Klann's Mechanical Spider handle heavier loads than Strandbeest and TrotBot?

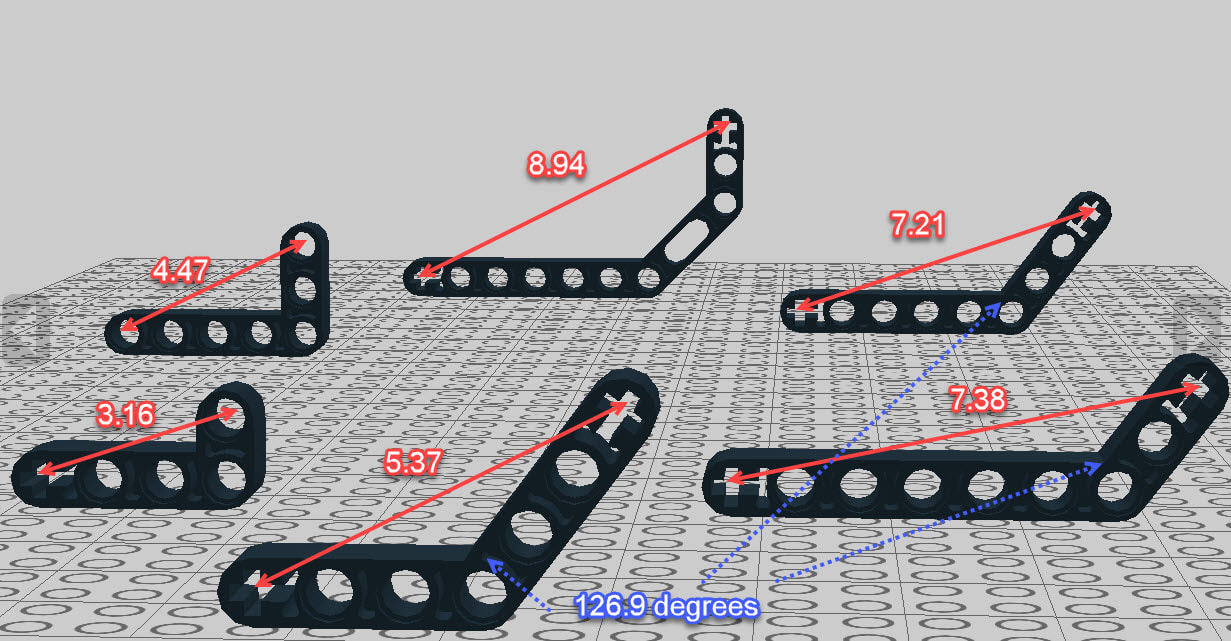
Walkers require very strong frames to handle the weight and torque. This is best accomplished through the use of triangles. Also, linkage attachments to frames need holes at precise locations, which often requires the use of right triangles. However, making right triangles is difficult as LEGO can only use integer numbers to construct them, such as 3,4,5 etc…

Since the 3,4,5 or 6,8,10 triangles might not work well with a walker frame, what other integer triangles, or almost integer triangles, can you come up with to create a stronger frame?

Alternatively, how could we use LEGO's bent lift-arms to create sturdy right triangle-based frames? The parts and their lengths are below. 

Remember, when counting how long a LEGO beam is, the first hole is always counted as 0!  In other words, a beam with 9 holes has a length of 8.  If you don't count LEGO beam lengths in this way then you won't be able to use the Pythagorean Theorem or Law of Cosines to solve for which beams to use as diagonal members.

To handle the stress, we try to use LEGO's cam-shaped parts like in the image above, which have a greater resistance to bending than do linear parts.  With 8-legged walkers, the inner and outer legs need to be 180 degrees out of phase, so we simply connect two such cranks together to make the double length cranks required to put the legs 180 degrees out of phase.  Note: for large-scale walkers we don't recommend using double-length cranks between the inner and outer legs.  Instead, single-length cranks should be used to return to the axle's center of rotation, and this axle section should be supported with diagonal beams to the support rods.  Then, another single-length crank is used to put the outer legs 180 degrees out of phase from the inner legs.  A simple example of this is shown in the animated GIF at the top of this post, with a yellow supporting beam between the left and right side's cranks.

​12-legged walkers have 3 leg-pairs on each side of the frame, and each of these leg-pairs needs to be 120 degrees out of phase with its adjacent leg-pairs.  So, adjacent cranks need to be 120 degrees out of phase, like in the simulation of TrotBot below.  

The only LEGO part we found with an 120 degree angle was the Technic Rotor 3 Blade Liftarm shown below, which required additional parts to make into cranks of sufficient length, added width to the walker, and the resulting crank was weak.

Can you come up with a better solution?
​
​(spoiler alert - one possible solution is presented further down)

​
​Below is one idea that utilizes triangles to make sturdy, 120 degree cranks with a width of 2 LEGO beams. 

​You can make an equilateral triangle with 3 Technic beams of the same length.

Add a 2nd equilateral triangle to it to create a 120 degree angle:

To transfer the rotation from one axle to another, LEGO parts with cross-shaped holes are needed.  Below is one idea for making 120 degree cranks of length 4.  The white and yellow 3-hole beams have a tight fit, but the resulting crank is sturdy.  ​NOTE:  The tight fit of the 3-hole beams increases the 120 degree angle slightly, which doesn't impact walking performance much but can be avoided by filing slightly the end of the 3 hole beams where they press against the gray beams.

Below shows how to orient the 3x7 bent beams to ensure all three cranks are 120 degrees out of phase:

Below is a video of a 12-legged version of Strider using this crank: