|
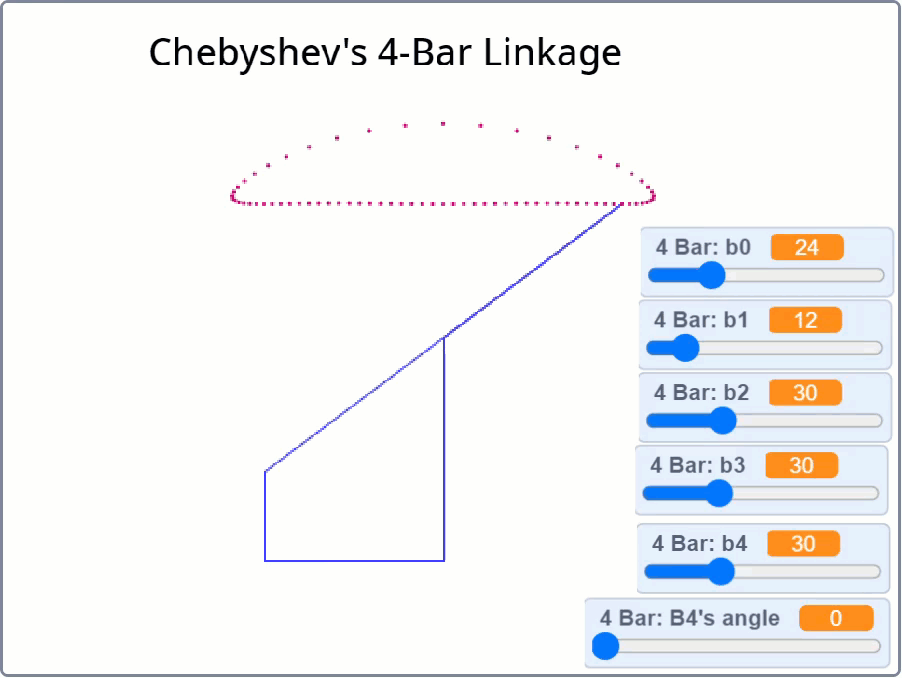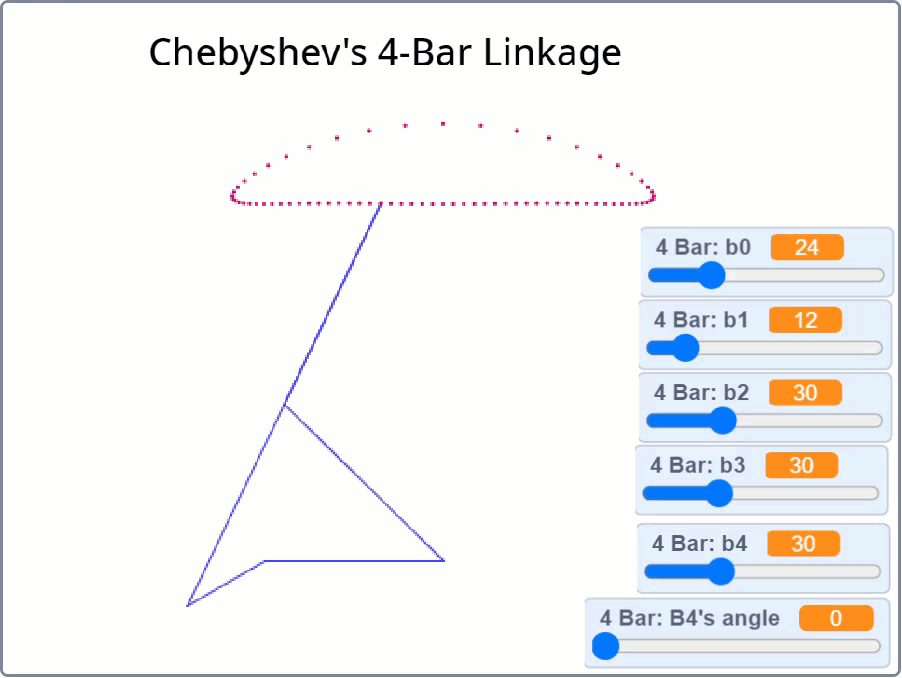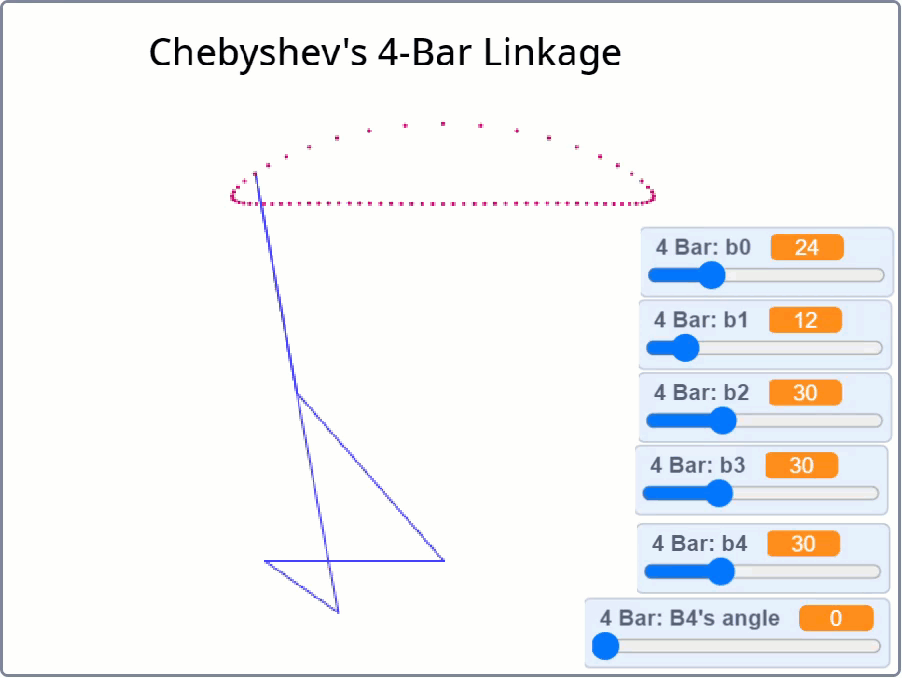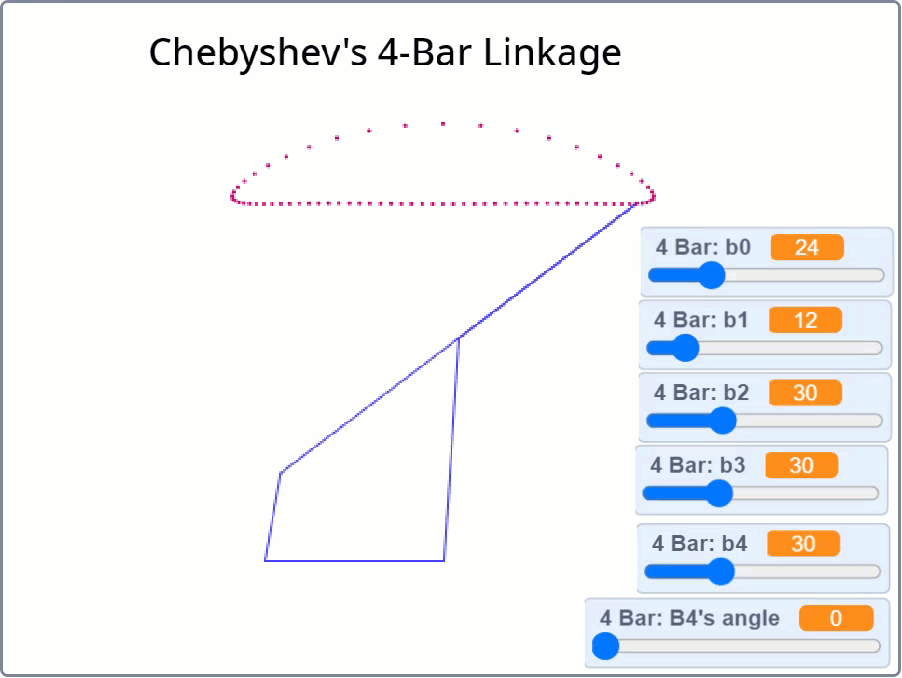
Posted by Oracid (Editors note: you can see more of Oracid's inspiring creations here) My goal is to explain simply how one can go from a usual 5 bars linkage to a 5 bars linkage with extension. The interest of this last mechanism is that it approaches the biological reality of a quadruped or a biped. In Fig.1, I show the equivalence between a usual 5 bars and its diamond-shaped reduction. The difference between these two linkages is located at the g bar which is fixed to the chassis. In the second linkage, the 5 bars turn into diamond with g = 0. Only the axis of rotation remains which fixes the 5 bars to the chassis.
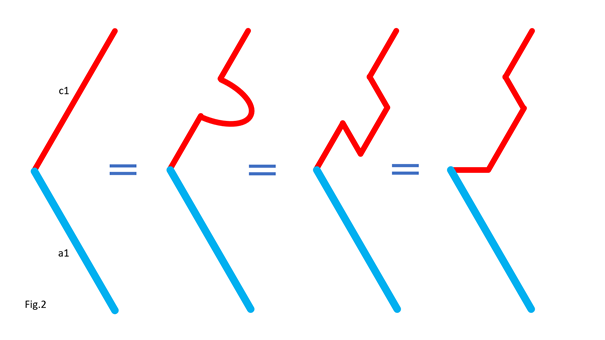
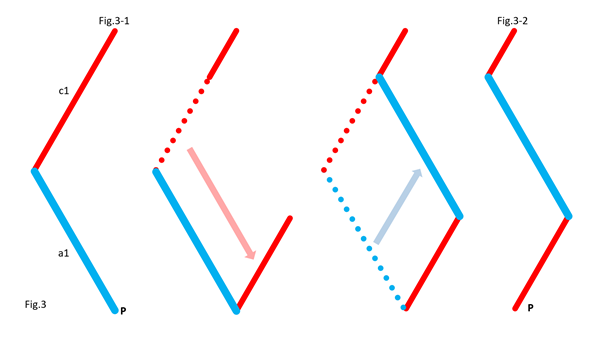
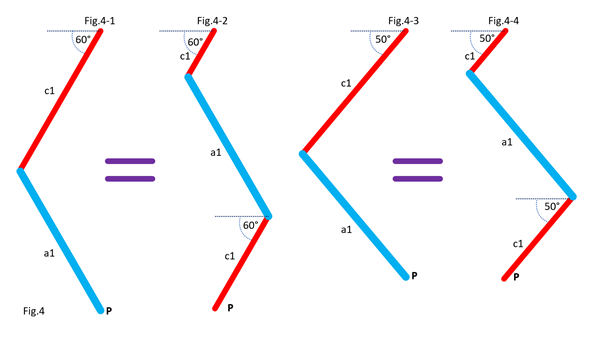
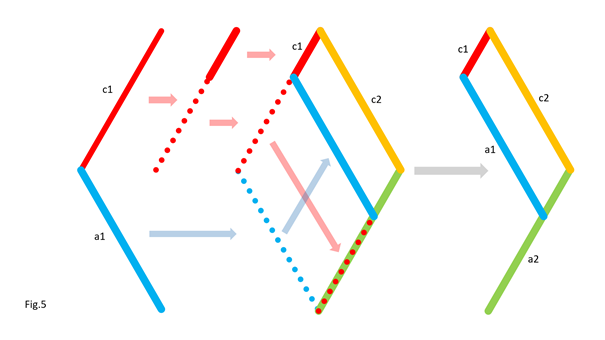
In Fig.2, I show that the shape of the bar c1 does not matter, provided that its ends keep the same position. For clarity, only the left side of the 5 bars is shown. In Fig.3, I show that we can move part of the line c1, provided that the parts are connected by an articulated bar forming part of a parallelogram. For clarity, only the left side of the 5 bars is shown. Here is how to go from the assembly in Fig.3-1 to the assembly in Fig.3-2 by translating part of the line c1 and the line a1. Notice that point P remains at the same position. In Fig.4, I show that whatever the angle of c1 with the horizontal in Fig.4-1 and Fig.4-3, there is respectively equivalence of the position of point P in Fig.4-2 and Fig.4-4. It is as if the two parts of c1 are one. This is because a1 and c2 (not shown, here) form a parallelogram which keeps the two parts of c1 at the same angle. For clarity, only the left side of the 5 bars is shown. In Fig.5, we can see a summary of the translations of the bars c1 and a1. The bar a1 is positioned at the end of the remaining part of the bar c1, while the “ghost” of the second part of c1 is translated and merged with a2. Fig.6 shows the result of the transformation and the equivalence of the two mechanisms. Also, check out Oracid's single DOF linkages, like this:
0 Comments
Leave a Reply. |
Categories
All
Archives
February 2023
|

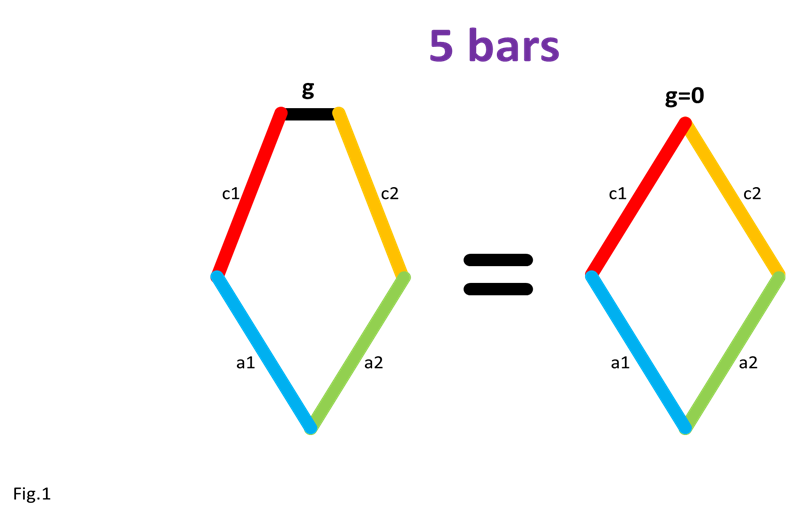
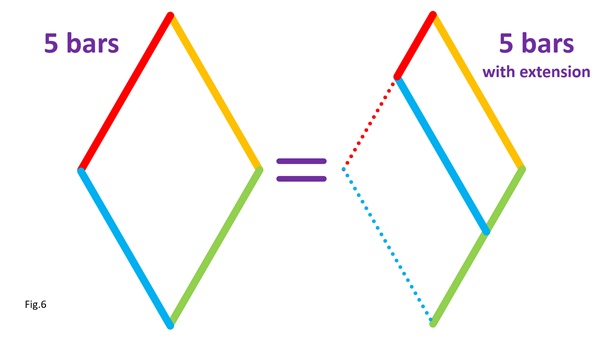
 RSS Feed
RSS Feed